Métricas de Evaluación

IIC 3633 - Sistemas Recomendadores

Denis Parra
Profesor Asistente, DCC, PUC CHile

Resumen + Próxima Semana

Ranking no personalizado: Ordenar items considerando el porcentage de valoraciones positivas y la cantidad total de valoraciones.
Filtrado Colaborativo: Basado en Usuario y en Items. Parámetros principales (K, métrica de distancia), ajustes por baja cantidad de valoraciones.
Slope One: Eficiencia y Escalabilidad por sobre la precisión
Métricas de Evaluación
Próxima Semana: Content-based filtering y práctico tarea

Evaluación Tradicional: Predicción de Ratings

MAE: Mean Absolute Error

\[MAE = \frac{\sum_{i=1}^{n}|\hat{r}_{ui}-r_{ui}|}{n}\]

MSE: Mean Squared Error

\[MSE = \frac{\sum_{i=1}^{n}{(\hat{r}_{ui}-r_{ui})^2}}{n}\]

RMSE: Root Mean Squared Error

\[RMSE = \sqrt{\frac{\sum_{i=1}^{n}{(\hat{r}_{ui}-r_{ui})^2}}{n}}\]

Evaluación de una Lista de Recomendaciones

Si consideramos los elementos recomendados como un conjunto \(S\) y los elementos relevantes como el conjunto \(R\), tenemos:

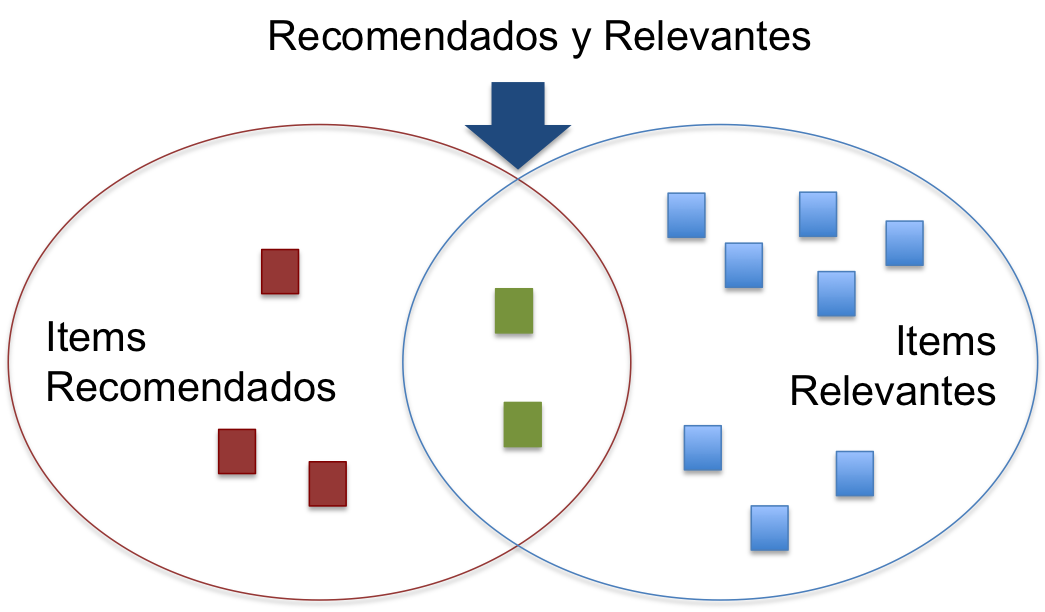
Luego, Precision es:

\[Precision = \frac{|Recomendados \cap Relevantes|}{|Recomendados|}, \textit{y}\]

\[Recall = \frac{|Recomendados \cap Relevantes|}{|Relevantes|}\]

Ejemplo 1: Precision y Recall

Si bien la lista de recomendaciones está rankeada, para estas métricas la lista se entiende más bien como un conjunto.

\[Precision = ??\]

\[Recall = ??\]

\[Precision = ??\]

\[Recall = ??\]

Ejemplo 1: Precision y Recall

\[Precision = \frac{5}{10} = 0,5\]

\[Recall = \frac{5}{20} = 0,25\]

\[Precision = \frac{3}{5} = 0,6\]

\[Recall = \frac{3}{20} = 0,15\]

Compromiso entre Precision y Recall

Al aumentar el Recall (la proporción de elementos relevantes) disminuimos la precision, por lo cual hay un compromiso entre ambas métricas.

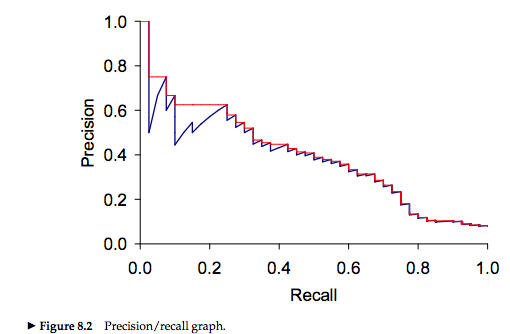
Por ello, generalmente reportamos la media harmónica entre ambas métricas: \[F_{\beta=1} = \frac{2*Precision*Recall}{P+R}\]

Ref: http://nlp.stanford.edu/IR-book/pdf/08eval.pdf

De evaluación de Conjuntos a Ranking

Mean Recicropal Rank (MRR)
Precision@N
MAP
Rank score
DCG
nDCG

Mean Reciprocal Rank (MRR)

Consideramos la posición en la lista del primer elemento relevante.

\[MRR = \frac{1}{r}, \textit{donde r: ranking del 1er elemento relevante}\]

\[MRR_1 = ??\]

\[MRR_2 = ??\]

Problema: Usualmente tenemos más de un elemento relevante!!

Mean Reciprocal Rank (MRR)

Consideramos la posición en la lista del primer elemento relevante.

\[MRR = \frac{1}{r}, \textit{donde r: ranking del 1er elemento relevante}\]

\[MRR_1 = \frac{1}{2} = 0,5\]

\[MRR_2 = \frac{1}{2} = 0,5\]

Problema: Usualmente tenemos más de un elemento relevante!!

Precision at N (P@N)

Corresponde a la \(precision\) en puntos específicos de la lista de items recomendados. En otras palabras, dado un ranking específica en la lista de recomendaciones, qué proporción de elementos relevantes hay hasta ese punto

\[Precision@n = \frac{\sum_{i = 1}^n{Rel(i)}}{n}, \textit{donde } Rel(i) = 1 \textit{si elemento es relevante}\]

\[Precision@5 = ??\]

Precision at N (P@N)

\[Precision@n = \frac{\sum_{i = 1}^n{Rel(i)}}{n}, \textit{donde } Rel(i) = 1 \textit{si elemento es relevante}\]

\[Precision@5 = \frac{2}{5} = 0,4\]

\[Precision@5 = \frac{3}{5} = 0,6\]

Pro: permite evaluar topN; Problema: aún no permite una evalución orgánica del los items con \(ranking < n\).

Mean Average Precision (MAP)

Average Precision (AP)

El AP se calcula sobre una lista única de recomendaciones, al promediar la precision cada vez que encontramos un elemento relevante, es decir, en cada recall point.

\[AP = \frac{\sum_{k \in K}{P@k \times rel(k)}}{|relevantes|}\]

donde \(P@k\) es la precision en el recall point \(k\), \(rel(k)\) es una función que indica 1 si el ítem en el ranking j es relevante (0 si no lo es), y \(K\) son posiciones de ranking con elementos relevantes.

MAP es la media de varias "Average Precision"

Considerando n usuarios en nuestro dataset y que a cada uno de dimos una lista de recomendaciones,

\[MAP = \frac{\sum_{u=1}^{n}{AP(u)}}{m}, \textit{donde m es el numero de usuarios.}\]

Mean Average Precision (MAP) - II

Como no siempre sabemos de antemano el número de relevantes o puede que hagamos una lista que no alcanza a encontrar todos los elementos relevantes, podemos usar una formulación alternativa** para Average Precision (AP@n)

\[AP@n = \frac{\sum_{k \in K}{P@k \times rel(k)}}{min(m,n)}\]

donde \(n\) es el máximo número de recomendaciones que estoy entregando en la lista, y \(m\) es el número de elementos relevantes.

Ejericio: calcule \(AP@n\) y luego \(MAP@n\), con \(n=10\), y \(m=20\) de:

** https://www.kaggle.com/wiki/MeanAveragePrecision

Rankscore

Rank Score se define como la tasa entre el Rank Score de los items correctos respecto al mejor Rank Score alcanzable por el usuario en teoría.

Parametros	Formula
h el conjunto de items correctamente recomendados, i.e. hits rank retorna la posición (rank) de un item T es el conjunto de items de interés \(\alpha\) es el ranking half life, i.e. un factor de reducción exponencial

DCG y nDCG

DCG: Discounted cummulative Gain

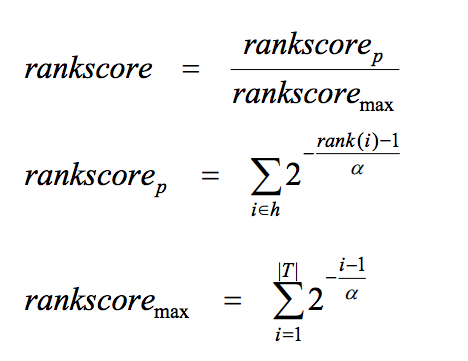\[DCG = \sum_i^p\frac{2^{rel_{i}}-1}{log_2(1+i)}\]

nDCG: normalized Discounted cummulative Gain, para poder comparar listas de distinto largo \[\mathit{nDCG} = \frac{DCG}{iDCG}\]

Ejercicio: Calcular nDCG para

Coverage

Como no a todos los usuarios se logran hacer recomendaciones, consideramos en la evaluación el User Coverage, el porcentaje de usuarios a los cuales se les pudo hacer recomendaciones.
Como no a todos los items pueden ser recomendaciones, consideramos en la evaluación el Item Coverage, el porcentaje de items que fueron recomendados al menos una vez.

Métricas para Tarea 1

Precision@10 = Recall@10, (ya que estamos "forzando" recomendados = relevantes)
MAP (en realidad, será MAP@10)
nDCG

Ejemplo con R

Paquete rrecsys

library(rrecsys)

data("mlLatest100k")

ML <- defineData(mlLatest100k, minimum = .5, maximum = 5, halfStar = TRUE)
ML

## Dataset containing 718 users and  8927 items.

R library(rrecsys)

# rowRatings(ML) : number of ratings per row 
# colRatings(ML) : number of ratings per columns

numRatings(ML)

## [1] 100234

sparsity(ML)

## [1] 0.9843619

R library(rrecsys)

# Ratings por usuario
hist( log(rowRatings(ML)) )

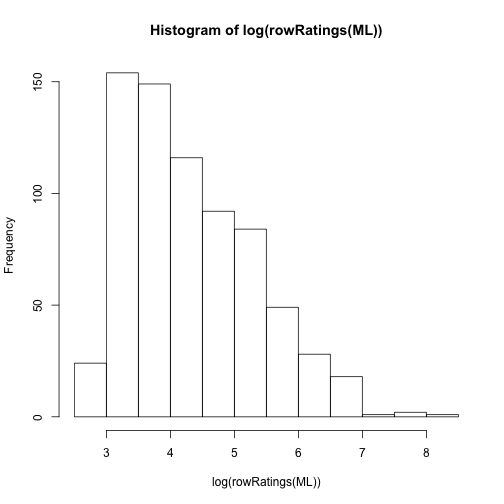
plot of chunk unnamed-chunk-5

R library(rrecsys)

plot(sort(rowRatings(ML), decreasing = T))

plot of chunk unnamed-chunk-6

Filtering dataset

subML <- ML[rowRatings(ML)>=40, colRatings(ML)>=30]
sparsity(subML)

## [1] 0.8683475

Recomendación No personalizada

# RecSys no personalizado ----
globAv <- rrecsys(subML, alg = "globalaverage")
# predict and recommend for all
p_globAv <- predict(globAv) # output: matriz de predicciones
r_globAv <- recommend(globAv, topN = 2) # output: lista con recomendaciones

Evaluación de predicciones

e <- evalModel(subML, folds = 5)
evalPred(e, 'globalaverage')

## 
## Fold: 1 / 5  elapsed. Time: 0.02280593 
## 
## 
## Fold: 2 / 5  elapsed. Time: 0.02660012 
## 
## 
## Fold: 3 / 5  elapsed. Time: 0.04744887 
## 
## 
## Fold: 4 / 5  elapsed. Time: 0.02128005 
## 
## 
## Fold: 5 / 5  elapsed. Time: 0.02667189 
## 
## The model was trained on the dataset using  globalAverage algorithm.

##               MAE      RMSE globalMAE globalRMSE
## 1-fold  0.8208376 0.9768961 0.8020253   1.007941
## 2-fold  0.8190966 0.9703925 0.7953272   0.996439
## 3-fold  0.8306264 0.9869071 0.8050932   1.011743
## 4-fold  0.8394394 0.9964792 0.8064962   1.007534
## 5-fold  0.8366290 0.9930068 0.7991900   1.002777
## Average 0.8293258 0.9847363 0.8016264   1.005287

Evaluación de recomendación topN

evalRec(e, 'globalaverage', goodRating = 4, topN = 5)

## Evaluating top- 5  recommendation with  globalAverage .
## 
## Fold: 1 / 5  elapsed. Time: 0.155278 
## 
## 
## Fold: 2 / 5  elapsed. Time: 0.09362984 
## 
## 
## Fold: 3 / 5  elapsed. Time: 0.09240508 
## 
## 
## Fold: 4 / 5  elapsed. Time: 0.0922451 
## 
## 
## Fold: 5 / 5  elapsed. Time: 0.09173799 
## 
## The model was trained on the dataset using  globalAverage algorithm.
## Item coverage: 1.527615 %.
## 
## User coverage: 100 %.

##                TP       FP       TN       FN  precision     recall
## 1-fold  0.1592742 4.840726 833.2903 12.70968 0.03185484 0.02470612
## 2-fold  0.1794355 4.820565 833.1310 12.86895 0.03588710 0.02141615
## 3-fold  0.1431452 4.856855 833.3750 12.62500 0.02862903 0.02932543
## 4-fold  0.1330645 4.866935 833.2177 12.78226 0.02661290 0.02966589
## 5-fold  0.1491935 4.850806 833.0827 12.91734 0.02983871 0.02188431
## Average 0.1528226 4.847177 833.2194 12.78065 0.03056452 0.02539958
##                 F1      nDCG rankscore
## 1-fold  0.01625969 0.1925534 0.2228745
## 2-fold  0.01728055 0.2085054 0.2416831
## 3-fold  0.01559165 0.1842961 0.2096182
## 4-fold  0.01488790 0.1597289 0.1851920
## 5-fold  0.01316086 0.1826945 0.2107694
## Average 0.01543613 0.1855557 0.2140274

Referencias

Manning, C. D., Raghavan, P., & Schütze, H. (2008). Introduction to information retrieval (Vol. 1, p. 6). Cambridge: Cambridge university press.
Baeza-Yates, R., & Ribeiro-Neto, B. (1999). Modern information retrieval (Vol. 463). New York: ACM press.
Slides "Evaluating Recommender Systems" http://www.math.uci.edu/icamp/courses/math77b/lecture_12w/pdfs/Chapter%2007%20-%20Evaluating%20recommender%20systems.pdf

Métricas de Evaluación

IIC 3633 - Sistemas Recomendadores

TOC

En esta clase

Con respecto al paper sobre CF de Resnick et al. (1994)

Resumen + Próxima Semana

Evaluación Tradicional: Predicción de Ratings

MAE: Mean Absolute Error

MSE: Mean Squared Error

RMSE: Root Mean Squared Error

Evaluación de una Lista de Recomendaciones

Ejemplo 1: Precision y Recall

Ejemplo 1: Precision y Recall

Compromiso entre Precision y Recall

De evaluación de Conjuntos a Ranking

Mean Reciprocal Rank (MRR)

Mean Reciprocal Rank (MRR)

Precision at N (P@N)

Precision at N (P@N)

Mean Average Precision (MAP)

Average Precision (AP)

MAP es la media de varias "Average Precision"

Mean Average Precision (MAP) - II

Rankscore

DCG y nDCG

Ejercicio: Calcular nDCG para

Coverage

Métricas para Tarea 1

Ejemplo con R

R library(rrecsys)

R library(rrecsys)

R library(rrecsys)

Filtering dataset

Recomendación No personalizada

Evaluación de predicciones

Evaluación de recomendación topN

Referencias