Factorización Matricial para RecSys

IIC 3633 - Sistemas Recomendadores - PUC Chile

Denis Parra
Profesor Asistente, DCC, PUC CHile

Memo del Semestre

  • Tarea 1: Deadline nuevo, Jueves 8 de Septiembre.

  • Lecturas en el semestre: Ya fueron actualizadas en el sitio web del curso.

TOC

En esta clase

  1. Contexto Histórico (Background)
  2. SVD
  3. SVD en sistemas recomendadores
  4. FunkSVD: descenso del gradiente estocástico
  5. Ejemplo en R: rrecsys y Jester dataset
  6. Extensiones del modelo básico: biases, implicit feedback, concept drift
  7. Consideraciones para implementación en sistemas en producción

Background I


  • Los primeros trabajos que usaron factorización matricial en sistemas recomendadores datan de comienzos de los 2000 (Sarwar et al. 2000; Sarwar et al. 2002) y mostraron resultados promisorios, pero no fue sino hasta el Netflix Prize (2006-2009) que los métodos de factorización matricial se volvieron más populares.

  • El Blog Post de un participante del Netflix Prize, Simon Funk (http://sifter.org/~simon/journal/20061211.html), que describió su solución basado en un cálculo incremental de SVD usando regularización, basado en el trabajo de Gorrell et al. (2005), ha sido frecuentemente citado en trabajos de sistemas recomendadores.

Background II


  • El trabajo ganador del Netflix Prize se basa en una composición (blending) de varios modelos, pero la técnica de factorización matricial es la más importante junto con Restricted Boltzmann Machines; de hecho, fueron las únicas 2 que Netflix puson realmente en producción terminado el concurso.

  • De ahí en adelante, una gran parte de los trabajos en sistemas recomendadores se fundan en estos modelos factorización matricial, también llamados de factores latentes.

Introducción I

  • En el filtrado colaborativo usamos la noción de "lo que le gusta a usuarios similares a mí podría también gustarme".

Introducción II

  • En el los modelos de factores latentes, el objetivo es encontrar un embedding donde tanto usuarios como ítems puedan mapearse en conjunto.

Introducción III

  • Bajo el paradigma de factores latentes de usuarios e ítems, la predicción de ratings podría realizarse de esta manera:

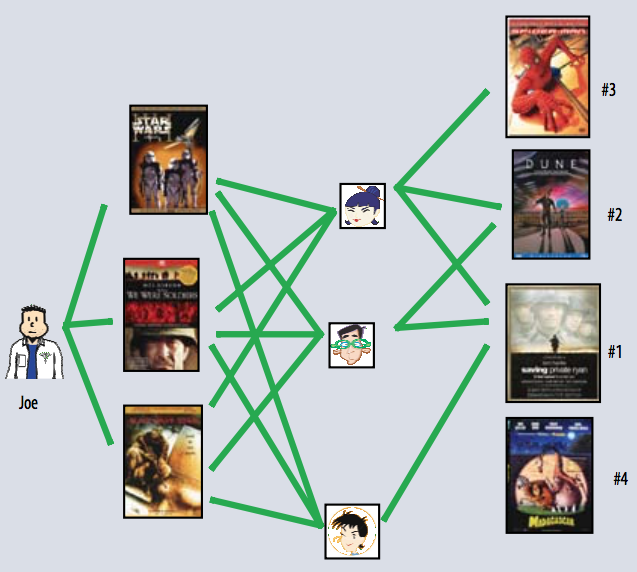
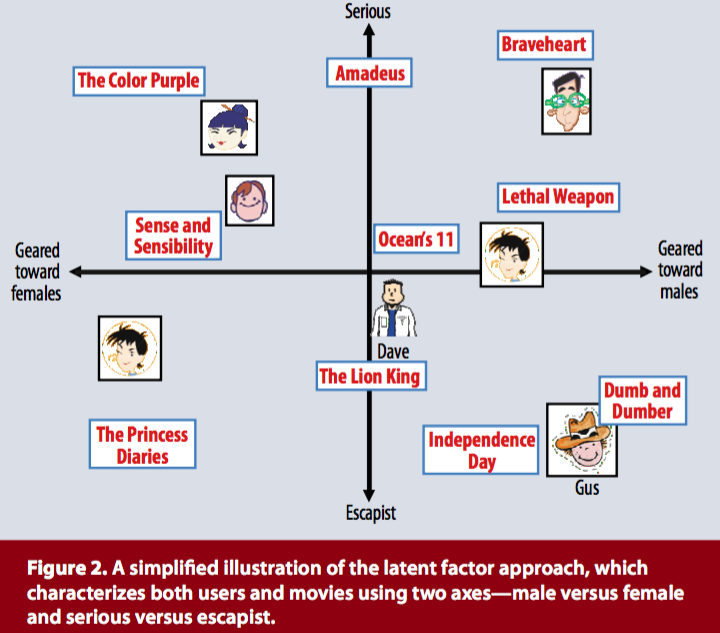
\[ r_{ui} = q_{i}^T \cdot p_u\]

  • donde
    • \(q_{i}\) corresponde al vector de factores del item \(i\) en el espacio latente y, análogamente,
    • \(p_u\) al vector de factores latentes del usuario \(u\).

Introducción IV

  • ¿Cómo encontrar los valores de los vectores \(q_i\) y \(p_u\)?

    • Opción 1: Usando directamente SVD, técnica de factorización matricial utilizada frecuentemente en recuperación de información (Latent Semantic Analysis).

    • Opción 2: Usar la siguiente función de pérdida, como un problema de optimización con regularización \(l_2\) que podemos resolver con stochastic gradient descent u otras técnicas.

      \[ \min_{q*,p*} \sum_{(u,i) \in K} (r_{ui} - q_{i}^T \cdot p_u)^2 + \lambda(||q_i||^2 + ||p_u||^2)\]

      donde \(K\) es el conjunto de pares \((u,i)\) para los cuales \(r_{ui}\) es conocido (training set).

SVD I

  • Teorema de diagonalización de matrices: Sea \(A\) una matriz \(m \times m\) cuadrada con valores reales, con \(m\) vectores propios linealmente independientes (en inglés eigenvectors). Luego, existe una descomposición \[A = USU^{-1}\], donde las columnas de \(U\) son los vectores propios de \(A\) y \(S\) es una matriz diagonal cuyas entradas son los valores propios de \(A\) en orden decreciente.

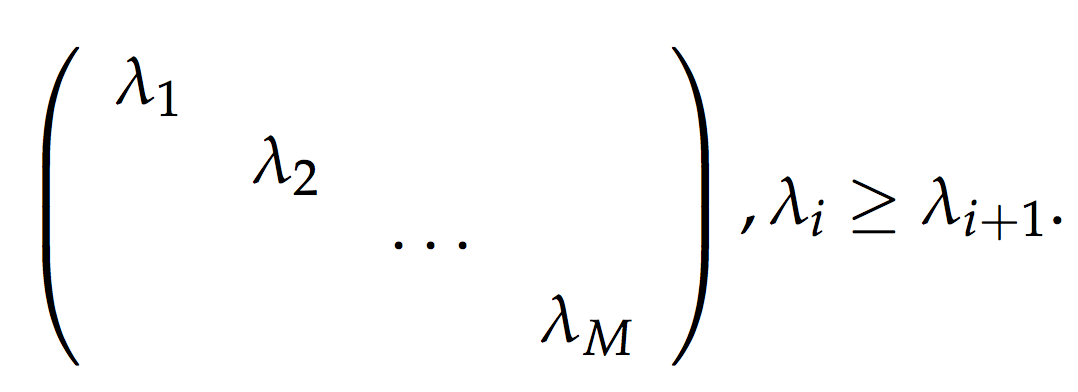
ref: Introduction to Information Retrieval, Manning et. al (2010)

SVD II

  • Teorema de diagonalización simétrica: Sea \(A\) una matriz \(m \times m\) cuadrada y simétrica con valores reales, con \(m\) vectores propios linealmente independientes. Luego, existe una descomposición \[A = QSQ^{T},\] donde las columnas de \(Q\) son los vectores propios ortogonales y normalizados de \(A\), y \(S\) es una matriz diagonal cuyas entradas son los valores propios de \(A\). Más aún, todas las entradas de Q son reales y tenemos que \(Q^{-1}=Q^{T}\).

    ref: Introduction to Information Retrieval, Manning et. al (2010)

SVD III

  • Teorema: Una matriz arbitraria \(A \in \Bbb{R}^{m \times n}\) permite una descomposición matricial de la forma:

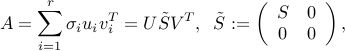
donde \(U \in \Bbb{R}^{m \times m}\) y \(V \in \Bbb{R}^{n \times n}\) son ambas matrices ortogonales, y la matriz {S} es diagonal:

\[S = diag = (\sigma_1 , \ldots, \sigma_r),\]

donde los números positivos \(\sigma_1 \ge \ldots \ge \sigma_r >0\) son únicos, y son llamados los valores singulares de \(A\). El número \(r \ge min(m,n)\) es igual al ranking de \(A\) y la tripleta \((U,\tilde{ {S}},V)\) es llamada la singular value decomposition (SVD) de \(A\).

Las primeras \(r\) columnas de \(U:u_i,i=1,\ldots,r\) (respectivamente \(V:v_i,i=1,\ldots,r\) ) son llamados los vectores izquierdos (resp. derechos) singulares de \(A\), y satisfacen:

\[Av_i = \sigma_i u_i, \;\; u_i^T A = \sigma_i v_i, \;\; i=1,\ldots,r.\]

ref: https://inst.eecs.berkeley.edu/~ee127a/book/login/thm_svd.html

Conectando los teoremas

  • Las matrices que usualmente usamos de usuario-item no son cuadradas ni simétricas.

  • Pero si consideramos el teorema SVD

    \[A = U\tilde{ {S}}V^T\]

    y luego que \(AA^T\) es una matriz cuadrada y simétrica, tenemos:

    \[AA^T = U\tilde{ {S}}V^T \; V\tilde{ {S}}U^T = U\tilde{ {S}}^2U^T\]

    y de forma análoga

    \[A^TA = V\tilde{ {S}}U^T \; U\tilde{ {S}}V^T = V\tilde{ {S}}^2V^T\]

    podemos calcular las matrices \(U\), \(V\) y \(\tilde{ {S}}\).

    ref: Introduction to Information Retrieval, Manning et. al (2010)

SVD Visualmente

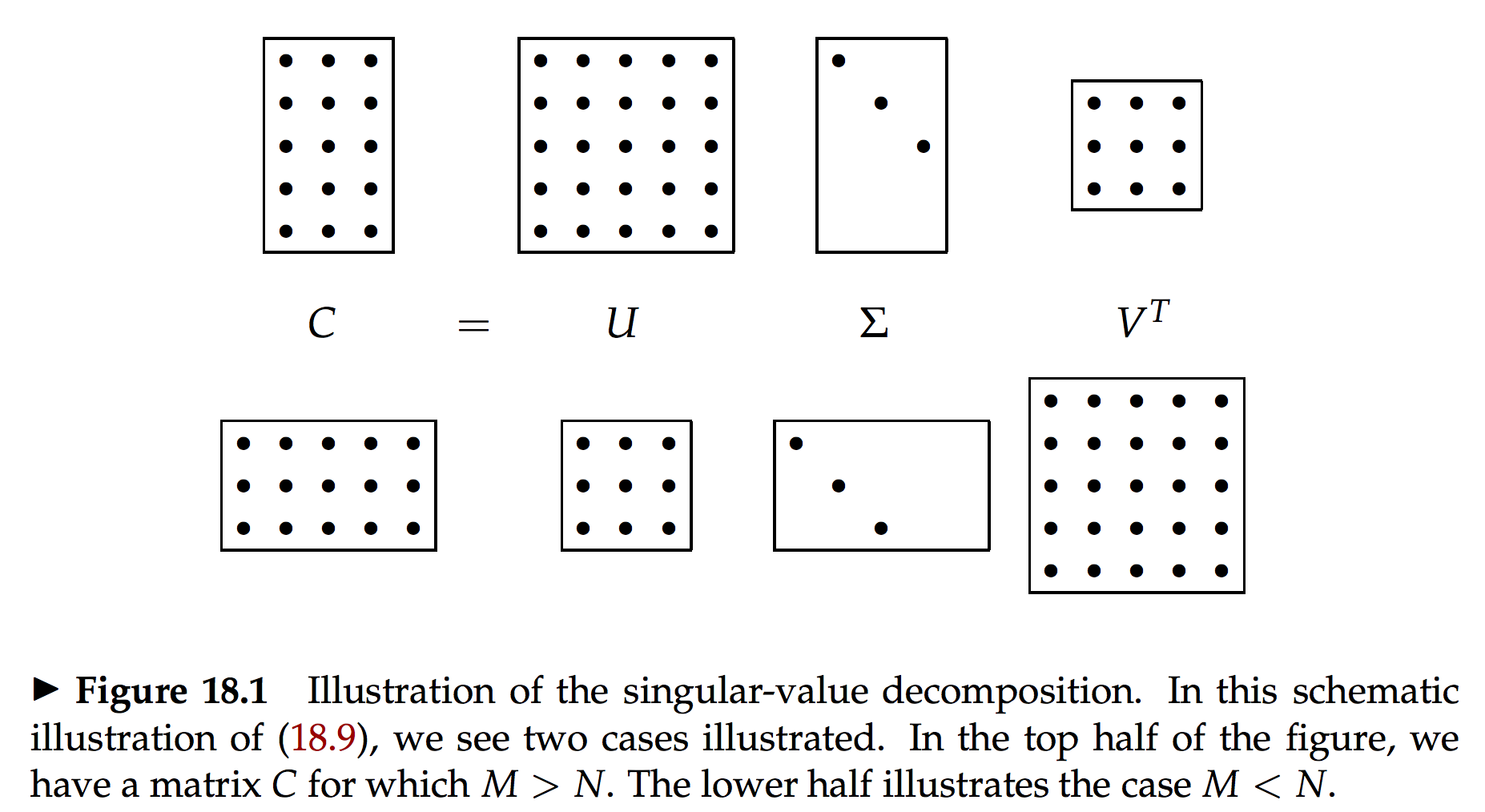
ref: Introduction to Information Retrieval, Manning et. al (2010)

Aproximación Low-rank

  • Dada una matriz \(A\) de \(m \times n\), deseamos encontrar una matriz \(A_k\) de ranking a lo más \(k\) y que minimice la norma Frobenius de la matriz de diferencias \(X = A - A_k\), definida como

\[||X||_F = \sqrt{\sum_{i=1}^{M}\sum_{j=1}^{n}X_{ij}^2}\]

  • la matriz \(low-rank\) aproximada \(A_k\) la podemos encontrar reemplazando por cero los valores singulares más pequeños de la matriz diagonal resultante de SVD:

SVD en Sistemas Recomendadores I

  • Sarwar et al (2000) presentaron un modelo para hacer recomendaciones usando SVD:

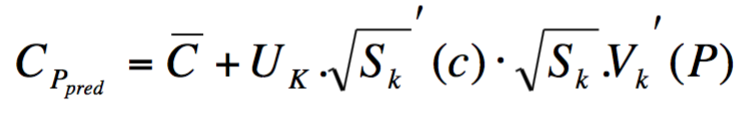
  • Una desventaja importante es cómo calcular la representación latente para nuevos usuarios.

    ref: Sarwar et al (2000). Application of Dimensionality Reduction in Recommender System -- A Case Study.

SVD en Sistemas Recomendadores II

  • Sarwar et al (2001) presentan un nuevo modelo para hacer recomendaciones usando SVD, y que permite imputar usuarios nuevos en el espacio latente:

  • ref: Incremental Singular Value Decomposition Algorithms for Highly Scalable Recommender Systems

Debilidades de SVD tradicional para RecSys

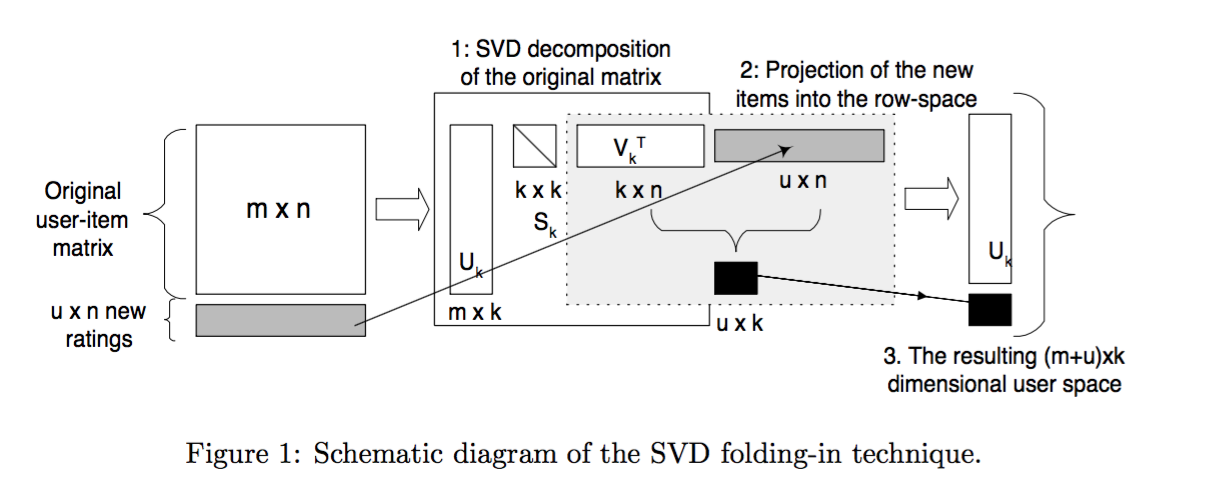
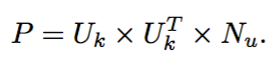
  • Calcular la SVD de una matriz es muy costoso, \(O(m^2n)\)

  • Problemas debido a la gran cantidad de celdas vacías en la matriz usuario-ítem obligaron a los autores en (Sarwar, 2000) a pre-llenarla.

  • El modelo tradicional de SVD no está definido cuando hay un conocimiento parcial de la matriz.

  • Utilizar un método convencional también corre el peligro de over-fitting.

Solución de Simon Funk: SVD incremental

  • Basada en Stochastic Gradient Descent, considerando trabajo de Gorrell (2005)

    • Itera sobre todos los ratings observados \(r_{ui}\), prediciendo \(r_{u,i}\) y calculando el error.

    • Luego actualiza los factores latentes usando las siguientes reglas de actualización.

Descenso del gradiente

  • Basado en ejemplo de Andrew Ng:

Derivación de las reglas de actualización I

  • Considerando

Derivación de las reglas de actualización II

  • Tenemos

Pseudocódigo para el algoritmo completo

Regularización

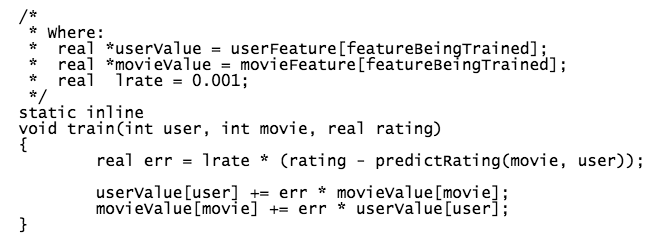
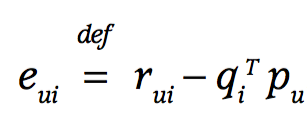
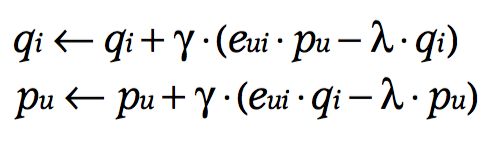
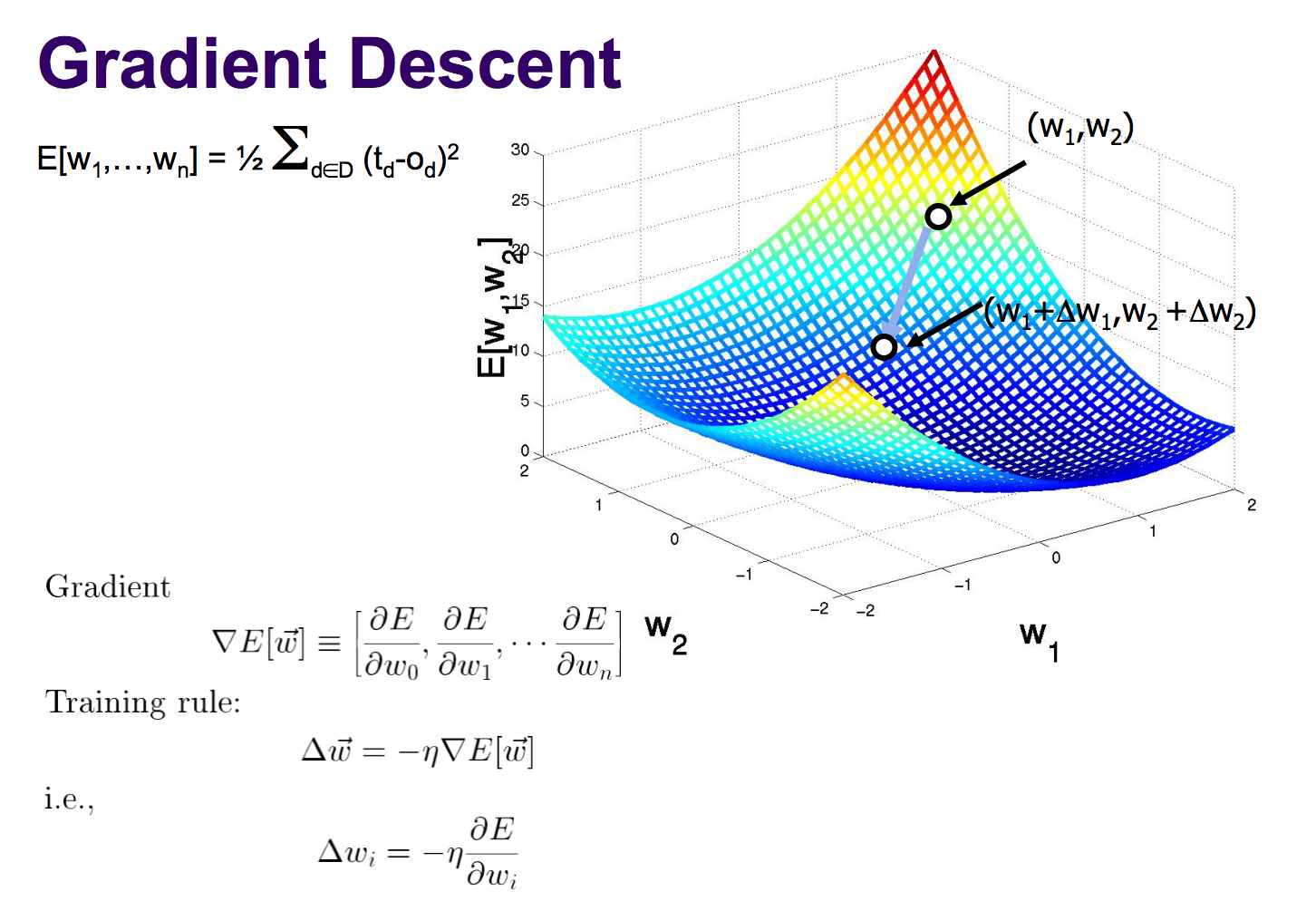
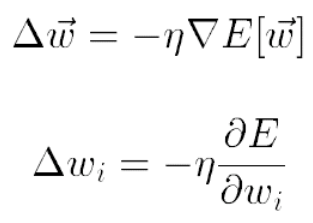
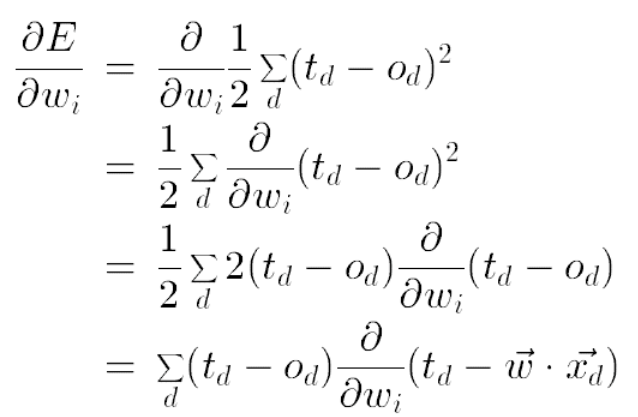
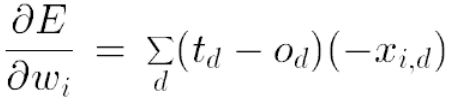
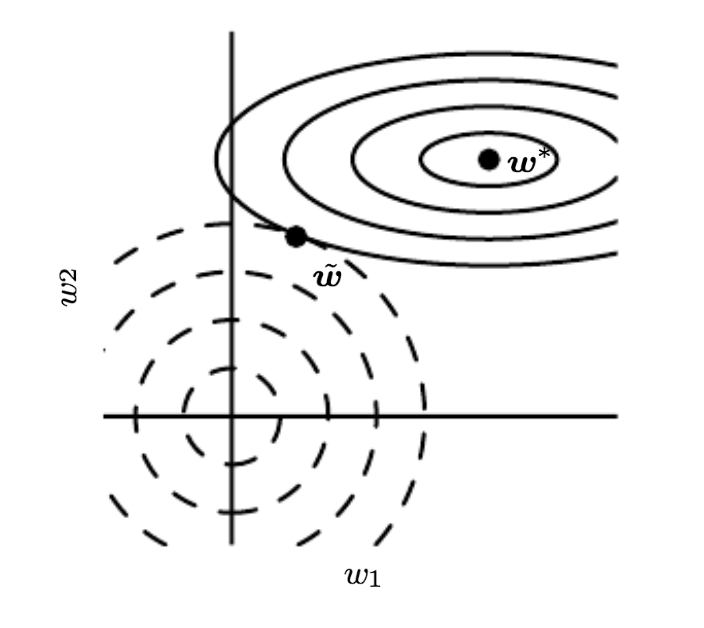
  • Al tener tan pocos datos la matriz (densidad del 1%-2%), el procedimiento corre el riesgo de sobre-entrenarse (over-fitting). Un regularizador permite penalizar valores muy altos de los coeficientes de los vectores latentes (Bishop, 2007;Goodfellow et al, 2016)

  • Por eso se agregan los términos \(||p_u||\) y \(||q_i||\) a la función de pérdida (loss function) \[\min_{q*,p*} \sum_{(u,i) \in K} (r_{ui} - q_{i}^T \cdot p_u)^2 + \lambda(||q_i||^2 + ||p_u||^2) \]

  • De esa forma, las reglas de actualización del SGD incluyen (siendo \(\gamma\) el learning rate):

Código del FunkSVD en paquete rrecsys I

Código del FunkSVD en paquete rrecsys II

Ejemplo de recomendaciones de bromas

Extensiones I

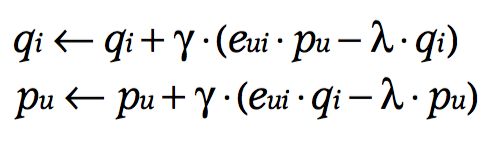
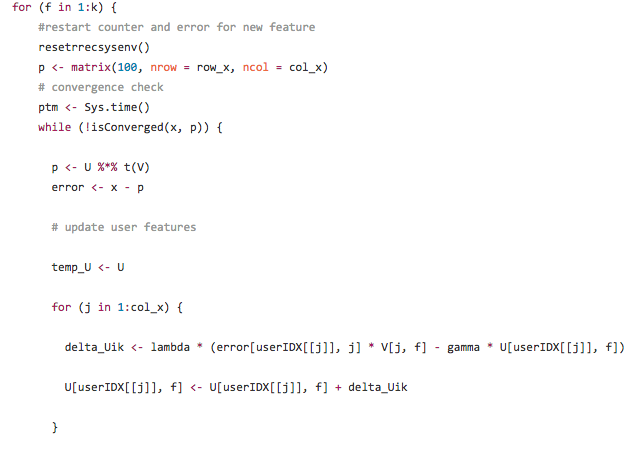
  • El modelo de Koren et al. para el Netflix prize incorpora los biases de usuarios e items:

Extensiones II

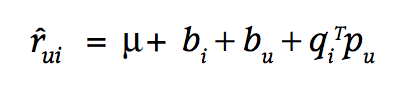
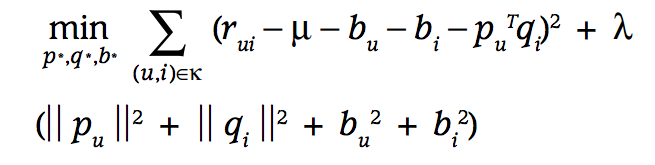
  • Luego de incluye información implícita en el modelo incorporando \(N(u)\)

Extensiones III

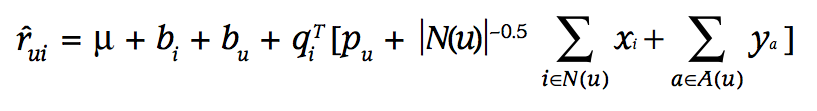
  • Luego de incluye información temporal (concept drift)

Resultados Finales

Muchos nuevos modelos!

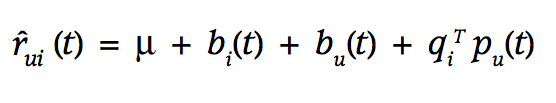
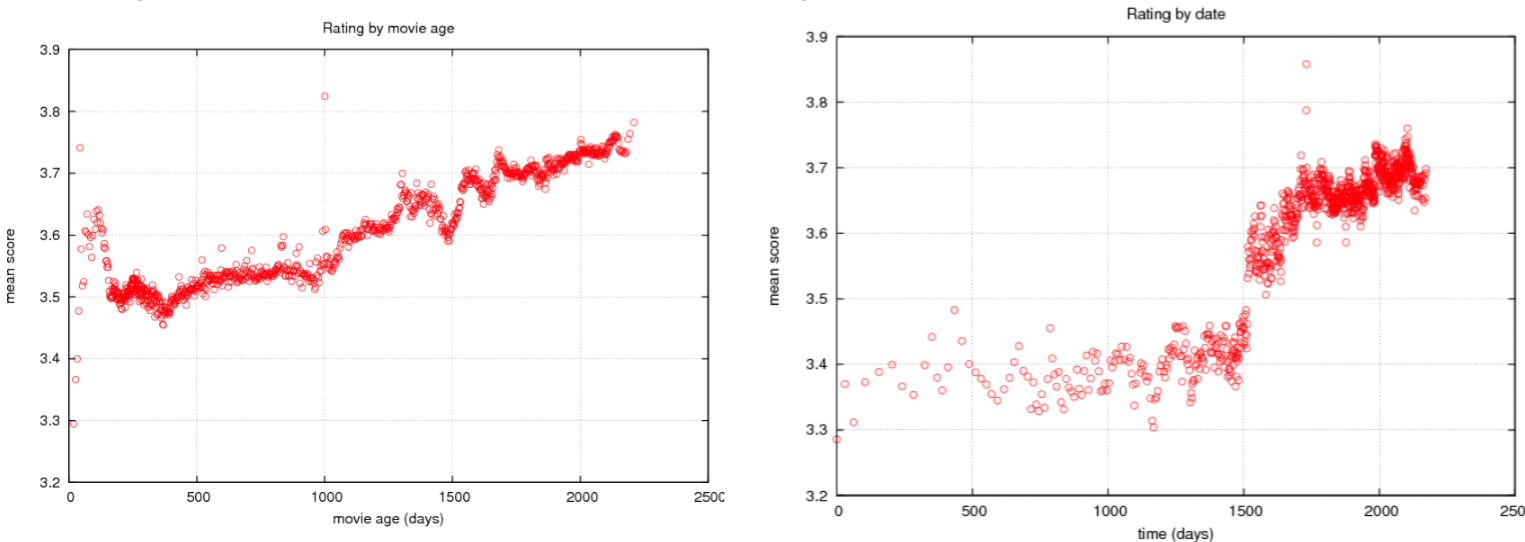
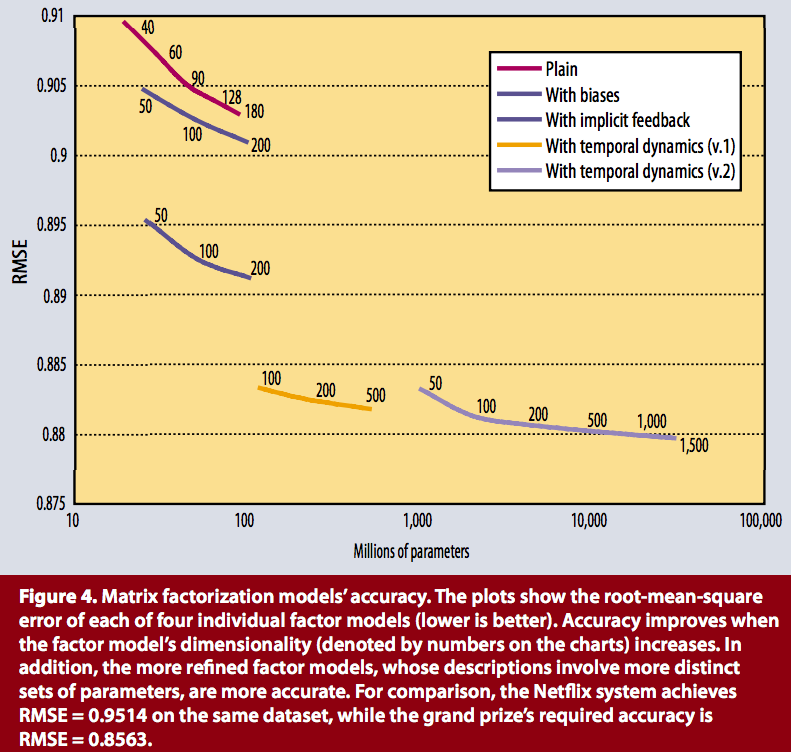
  • Collaborative Filtering for Implicit Feedback Datasets

  • BPR

  • Factorization Machines

  • Tensor Factorization (context)

  • NMF

  • SLIM

¿Implementación en el Mundo Real?

Referencias

  • Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2000). Application of Dimensionality Reduction in Recommender System -- A Case Study
  • Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2002). Incremental singular value decomposition algorithms for highly scalable recommender systems. In Fifth International Conference on Computer and Information Science (pp. 27-28).
  • Manning, C. D., Raghavan, P. and Schütze, H. (2008). Introduction to Information Retrieval. Cambridge University Press, New York, NY, USA.
  • Gorrell, G., & Webb, B. (2005). Generalized hebbian algorithm for incremental latent semantic analysis. In INTERSPEECH (pp. 1325-1328).
  • Funk, S. (2006). Try this at home. Blog post: http://sifter.org/~simon/journal/20061211.html. December11.
  • Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix factorization techniques for recommender systems. Computer, 42(8), 30-37. Chicago
  • recommenderlab https://cran.r-project.org/web/packages/recommenderlab/vignettes/recommenderlab.pdf
  • rrecsys https://cran.r-project.org/web/packages/rrecsys/index.html

Referencias II