Métricas de Evaluación

En esta clase

1. Resumen + Próxima Semana
2. Prediccion de Ratings: MAE, MSE, RMSE
3. Evaluacion via Precision-Recall
4. Metricas P@n, MAP,
5. Metricas de Ranking: DCG, nDCG,
6. Metricas en Tarea 1

• Ranking no personalizado: Ordenar items considerando el porcentage de valoraciones positivas y la cantidad total de valoraciones.

• Filtrado Colaborativo: Basado en Usuario y en Items. Parámetros principales (K, métrica de distancia), ajustes por baja cantidad de valoraciones.

• Slope One: Eficiencia y Escalabilidad por sobre la precisión

• Métricas de Evaluación

• Próxima Semana: Content-based filtering y tag-based recommenders

MAE: Mean Absolute Error

\[MAE = \frac{\sum_{i=1}^{n}|\hat{r}_{ui}-r_{ui}|}{n}\]

MSE: Mean Squared Error

\[MSE = \frac{\sum_{i=1}^{n}{(\hat{r}_{ui}-r_{ui})^2}}{n}\]

RMSE: Root Mean Squared Error

\[RMSE = \sqrt{\frac{\sum_{i=1}^{n}{(\hat{r}_{ui}-r_{ui})^2}}{n}}\]

Si consideramos los elementos recomendados como un conjunto \(S\) y los elementos relevantes como el conjunto \(R\), tenemos:

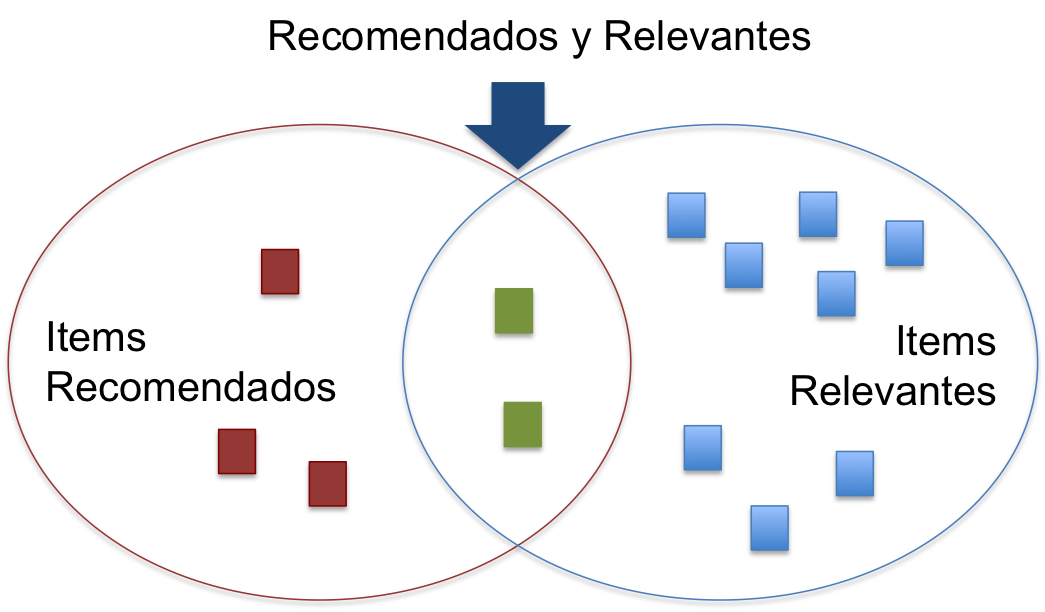
Luego, Precision es:

\[Precision = \frac{|Recomendados \cap Relevantes|}{|Recomendados|}, \textit{y}\]

\[Recall = \frac{|Recomendados \cap Relevantes|}{|Relevantes|}\]

Si bien la lista de recomendaciones está rankeada, para estas métricas la lista se entiende más bien como un conjunto.

\[Precision = ??\]

\[Recall = ??\]

\[Precision = ??\]

\[Recall = ??\]

\[Precision = \frac{5}{10} = 0,5\]

\[Recall = \frac{5}{20} = 0,25\]

\[Precision = \frac{3}{5} = 0,6\]

\[Recall = \frac{3}{20} = 0,15\]

Al aumentar el Recall (la proporción de elementos relevantes) disminuimos la precision, por lo cual hay un compromiso entre ambas métricas.

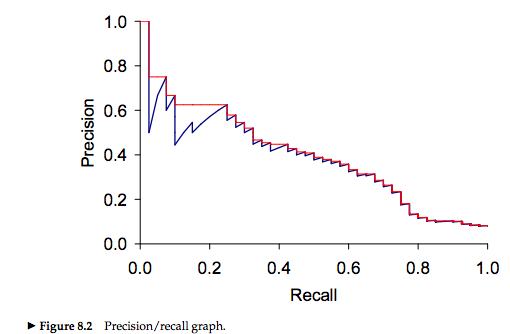
Por ello, generalmente reportamos la media harmónica entre ambas métricas: \[F_{\beta=1} = \frac{2*Precision*Recall}{P+R}\]

• Ref: http://nlp.stanford.edu/IR-book/pdf/08eval.pdf

• Mean Recicropal Rank (MRR)
• Precision@N
• MAP
• DCG
• nDCG

Consideramos la posición en la lista del primer elemento relevante.

\[MRR = \frac{1}{r}, \textit{donde r: ranking del 1er elemento relevante}\]

\[MRR_1 = \frac{1}{2} = 0,5\]

\[MRR_2 = \frac{1}{2} = 0,5\]

Problema: Usualmente tenemos más de un elemento relevante!!

Corresponde a la \(precision\) en puntos específicos de la lista de items recomendados. En otras palabras, dado un ranking específica en la lista de recomendaciones, qué proporción de elementos relevantes hay hasta ese punto

\[Precision@n = \frac{\sum_{i = 1}^n{Rel(i)}}{n}, \textit{donde } Rel(i) = 1 \textit{si elemento es relevante}\]

\[Precision@5 = \frac{2}{5} = 0,4\]

\[Precision@5 = \frac{3}{5} = 0,6\]

Pro: permite evaluar topN; Problema: aún no permite una evalución orgánica del los items con \(ranking < n\).

Average Precision (AP)

• El AP se calcula sobre una lista única de recomendaciones, al promediar la precision cada vez que encontramos un elemento relevante, es decir, en cada recall point.

\[AP = \frac{\sum_{k \in K}{P@k \times rel(k)}}{|relevantes|}\]

donde \(P@k\) es la precision en el recall point \(k\), \(rel(k)\) es una función que indica 1 si el ítem en el ranking j es relevante (0 si no lo es), y \(K\) son posiciones de ranking con elementos relevantes.

MAP es la media de varias "Average Precision"

• Considerando n usuarios en nuestro dataset y que a cada uno de dimos una lista de recomendaciones,

\[MAP = \frac{\sum_{u=1}^{n}{AP(u)}}{m}, \textit{donde m es el numero de usuarios.}\]

Como no siempre sabemos de antemano el número de relevantes o puede que hagamos una lista que no alcanza a encontrar todos los elementos relevantes, podemos usar una formulación alternativa** para Average Precision (AP@n)

\[AP@n = \frac{\sum_{k \in K}{P@k \times rel(k)}}{min(m,n)}\]

donde \(n\) es el máximo número de recomendaciones que estoy entregando en la lista, y \(m\) es el número de elementos relevantes.

• Ejericio: calcule \(AP@n\) y luego \(MAP@n\), con \(n=10\), y \(m=20\) de:

** https://www.kaggle.com/wiki/MeanAveragePrecision

• DCG: Discounted cummulative Gain

\[DCG = \sum_i^p\frac{2^{rel_{i}}-1}{log_2(1+i)}\]

• nDCG: normalized Discounted cummulative Gain, para poder comparar listas de distinto largo \[\mathit{nDCG} = \frac{DCG}{iDCG}\]

Ejercicio: Calcular nDCG para

• Precision@10 = Recall@10, (ya que estamos "forzando" recomendados = relevantes)
• MAP (en realidad, será MAP@10)
• nDCG

• Manning, C. D., Raghavan, P., & Schütze, H. (2008). Introduction to information retrieval (Vol. 1, p. 6). Cambridge: Cambridge university press.