Recomendador Slope One

En esta clase

1. Resumen últimas clases
2. Control de lectura próxima semana y Tarea
3. Recomendador Slope One
4. Ejemplo pequeño

• Ranking no personalizado: Ordenar items considerando el porcentage de valoraciones positivas y la cantidad total de valoraciones.

• Filtrado Colaborativo basado en el usuario: buscar K usuarios más parecidos, luego predecir rating de items no consumidos por el active user.

• Filtrado Colaborativo basado en items: pre-calcular directamente similaridad entre items co-rated, saltándose búsqueda de K-vecindario.

Preguntas tipo

• Describir la idea y fundamento del método o algoritmo
• Escribir las fórmulas para cálculo de similaridad y la predicción
• Calcular un ejemplo pequeño (traer calculadora)
• Identificar pros y contras de cada método
• Efecto de diferentes parámetros

• How not to sort by Average Rating, Evan Miller Blog
• Resnick, P., Iacovou, N., Suchak, M., Bergstrom, P., & Riedl, J. (1994, October). GroupLens: an open architecture for collaborative filtering of netnews. In Proceedings of the 1994 ACM conference on Computer supported cooperative work (pp. 175-186). ACM.
• Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2001, April). Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conference on World Wide Web (pp. 285-295). ACM.
• Herlocker, J. L., Konstan, J. A., Borchers, A., & Riedl, J. (1999, August). An algorithmic framework for performing collaborative filtering. In Proceedings of the 22nd annual international ACM SIGIR conference on Research and development in information retrieval (pp. 230-237).
• Lemire, D., & Maclachlan, A. (2005, April). Slope One Predictors for Online Rating-Based Collaborative Filtering. In SDM (Vol. 5, pp. 1-5).

• Será anunciada el martes 19 de Agosto (Próxima semana)
  
• Considerando un dataset que nosotros les entregaremos, deben implementar los recomendadores vistos hasta ahora y elegir el mejor. Con ese "mejor recomendador" realizarán dos tareas sobre un Hold Out dataset: predecir ratings y generar una lista topN de recomendaciones.

Predicción	Recomendación Top-N

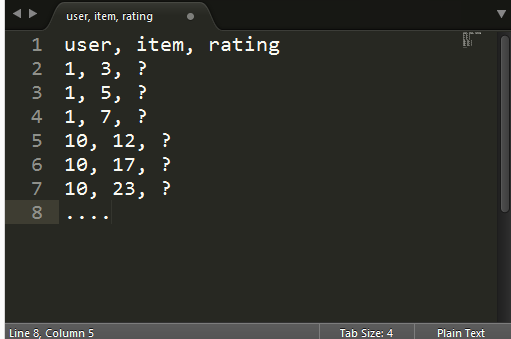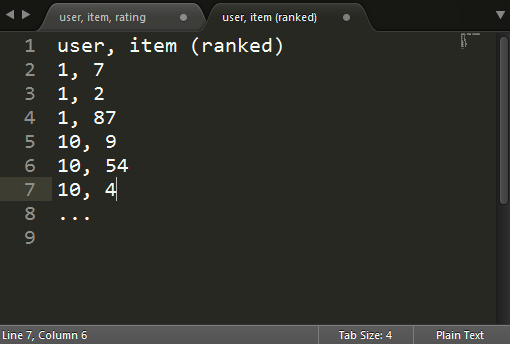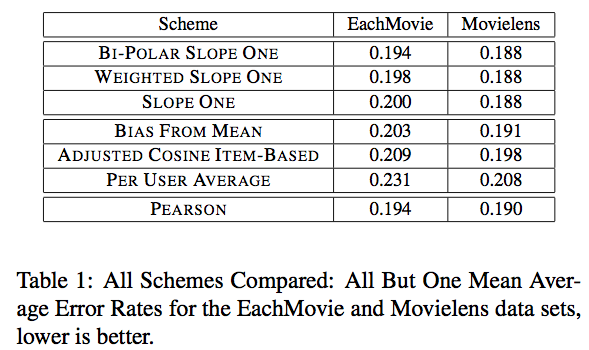
Lemire, D., & Maclachlan, A. (2005, April). Slope One Predictors for Online Rating-Based Collaborative Filtering. In SDM (Vol. 5, pp. 1-5).

Los autores se enfocan en 5 objetivos:

1. Fácil de Implementar y mantener
2. Actualizable en línea: nuevos ratings deberían cambiar las predicciones rápidamente.
3. Eficiente al momento de consulta: costo principal debería llevarlo el almacenamiento.
4. Funciona con poco feedback del usuario
5. Razonablemente preciso, dento de ciertos rangos en los que una pequeña ganancia en exactitud no signifique un gran sacrificio de simplicidad y escalabilidad.

Si observamos las diferencias de ratings entre pares de items, podemos hacer una predicción.

• Ecuación Lineal de Pendiente uno

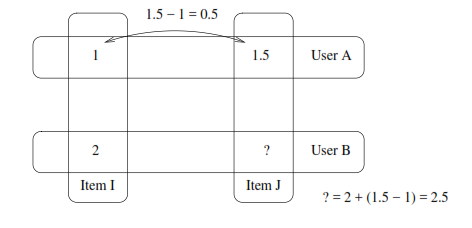
\[ f(x) = x + b \]

• Si tenemos dos vectores con ratings \(v_i\) y \(w_i\) donde \(i=1..n\), buscamos el mejor predictor de la forma \(f(x)=x+b\) para predecir \(w\) usando \(v\). Luego, tratamos de minimizar la expresión

\[\sum_{i=1}^{n}{(v_i+b-w_i)^2}\]

• Derivando con respecto a \(b\) e igualando la expresión a 0, nos queda

\[b=\frac{\sum_i{(v_i-w_i)}}{n}\]

• Implementación Normal \[dev_{j,i}=\sum_{u \in S_{j,i(\chi)}}{\frac{u_j-u_i}{card(S_{j,i}(\chi))}},\ desviacion\ promedio\ entre\ dos\ items\ i,\ j\] \[P(u)_j = {\frac{1}{card(R_j)}}{\sum_{i \in R_j}{(dev_{j,i}+u_i)}},\ prediccion\ en\ base\ a\ varios\ items\ i\] \[P(u)_j^{S1} = \bar{u}+{\frac{1}{card(R_j)}}{\sum_{i \in R_j}{dev_{j,i}}},\ aproximacion\ cuando\ R_j S(u)\]
• Métodos de Ponderación
  • Weighted
  • Bipolar

• Weighted Slope One: Algunos pares de items han sido evaluados por muchos usuarios, otros no tanto

\[P(u)_j^{wS1} = \frac{\sum_{i \in S(u)-\{j\}}{(dev_{j,i}+u_i)c_{j,i}} }{\sum_{i \in S(u)-\{j\} }{c_{j,i}}},\ donde\ c_{i,j} = card(S_{j,i}(\chi))\]

• Bi-Polar: los items evaluados positivamente son considerados distintos a los evaludos negativamente.

\[dev_{j,i}^{like}=\sum_{u \in S_{j,i(\chi)}^{like}}{\frac{u_j-u_i}{card(S_{j,i}^{like}(\chi))}},\text{ desviacion media entre dos items liked}\] \[p_{j,i}^{like}=dev_{j,i}^{like}+u_i \text{, y de modo similar, } p_{j,i}^{dislike}=dev_{j,i}^{dislike}+u_i\]

Combinando ambos, like y dislike, la predicción queda:

\[P(u)_j^{bpS1} = \frac{\sum_{i \in S(u)^{like}-\{j\}}{p_{j,i}^{like}c_{j,i}^{like}} + \sum_{i \in S(u)^{dislike}-\{j\}}{p_{j,i}^{dislike}c_{j,i}^{dislike}}}{\sum_{i \in S(u)^{like}-\{j\} }{c_{j,i}^{like}} + \sum_{i \in S(u)^{dislike}-\{j\} }{c_{j,i}^{dislike}}}\]

(A pedido de A.P.)

• Usando Weighted Slope One, calcule qué rating le daría U3 a Spiderman*:

• Usando Weighted Slope One, calcule qué rating le daría U3 a Spiderman*:

1. Desviación promedio entre Spiderman y Batman (en la resta, primero Spiderman) \[dev_{j,i}=\sum_{u \in S_{j,i(\chi)}}{\frac{u_j-u_i}{card(S_{j,i}(\chi))}},\text{j: Spiderman, i:Batman}\]
2. Desviación promedio Spider Man y Harry Potter (en la resta, primero Spiderman) \[dev_{j,i}=\sum_{u \in S_{j,i(\chi)}}{\frac{u_j-u_i}{card(S_{j,i}(\chi))}},\text{j: Spiderman, i:Harry Potter}\]
3. Predicción: Usando el rating que el usuario U3 le dio a Batman y a Harry Potter, calcular rating de U3 a Spiderman

\[P(u)_j^{wS1} = \frac{\sum_{i \in S(u)-\{j\}}{(dev_{j,i}+u_i)c_{j,i}} }{\sum_{i \in S(u)-\{j\} }{c_{j,i}}},\ donde\ c_{i,j} = card(S_{j,i}(\chi))\]

• Desviación promedio entre Spiderman y Batman (en la resta, primero Spiderman)

\[[(4-3)+(4-2)]/2=1,5\]

• Desviación promedio SpiderMan y Harry Potter (en la resta, primero Spiderman)

\[[(4-5)]/1=-1\]

• Predicción: Usando el rating que el usuario U3 le dio a Batman y a Harry Potter, calcular rating de U3 a Spiderman
  • Usando Batman (rating the U3 a Batman + desviación)
    \(r=2+1,5=3,5\)
  • Usando Harry Potter (rating the U3 a Harry Potter + desviación)
    \(r=4-1=3\)
  • Considerando ambas predicciones y la cantidad de muestras usadas en cada uno
    \((3,5*2 + 3*1)/(2+1)=3,33\)

• Lemire, D., & Maclachlan, A. (2005, April). Slope One Predictors for Online Rating-Based Collaborative Filtering. In SDM (Vol. 5, pp. 1-5).
• *Ejercicio sacado de http://www.slideshare.net/irecsys/slope-one-recommender-on-hadoop-15199798