Item-Based CF

En esta clase

1. Resumen Clase anterior
2. Por qué otra versión de CF?
3. Filtrado Colaborativo Basado Items (Sarwar et al. 2010)
4. Referencias

Recommender Systems aim to help a user or a group of users in a system
to select items from a crowded item or information space.

• Ranking no personalizado: Varias opciones. Si consideramos que los ítems a rankear tienen valoraciones positivas y negativas, el ranking ideal debería considerad la proporción de positivas y la cantidad de muestras consideradas: una opción es el límite inferior del Intervalo de Confianza del Wilson Score, para un parámetro Bernoulli.

• Filtrado Colaborativo (Basado en el usuario): Buscamos los K usuarios más parecidos a nuestro "active" o "center" user (K-NN). Luego, hacemos predicción de items que los vecinos han consumido, pero que el "active user" no ha consumido aún.

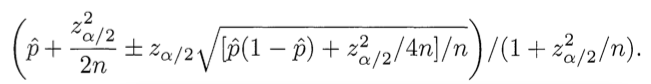
\[Similaridad(u,v) = w(u,v), v \in K\] \[\hat{p}_{u,i} = \bar{r}_u + \alpha \sum_{v \in N(u)}{w(u,v)(r_{v,i} - \bar{r}_v)}\]

Balance entre Escalabilidad y Exactitud

• Exactitud: Mientras más vecinos \(K\) consideramos (bajo cierto umbral), mejor debería ser mi clasificación (Lathia et al. 2008)

• Escalabilidad: Pero mientras más usuarios \(n\) existen en el sistema, mayor es el costo de encontrar los K vecinos más cercanos, ya que K-NN es \(O(dnk)\). Considerando un sitio con millones de usuarios, calcular las recomendaciones usando este método \(memory-based\) se hace poco sustentable.

Más aún, hay que lidiar con otros problemas

• Dispersión (Sparsity): La baja densidad de los datos hace que el Filtrado Colaborativo basado en el usuario sufra de "Cold-start" (usuarios con pocos ratings o historial de acciones) y también del "new item problem" (items nuevos que nadie los ha consumido)

• Model-based methods: Redes Bayesianas (ideales en casos en que las preferencias del usuario no cambian tan a menudo), Reducción de dimensionalidad (estado del arte, pero tiene algunos costos de implementación, especialmente en "tunear" los parámetros)

• Clustering, aunque tienen como efecto producir recomendaciones "no tan personalizadas" y, disminuir la exactitud de las predicciones en algunos casos (Breese et al. 1998)

• Graph-based methods: Horting, Random Walks, Spread of activation. Son menos precisos, pero contribuyen a dar mayor diversidad a las recomendaciones

• Item-base recommendation: Revisar user-based (precisión + simpleza) y escalarlo :-)

User-Based	Item-Based

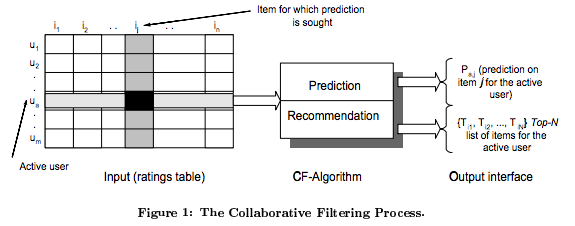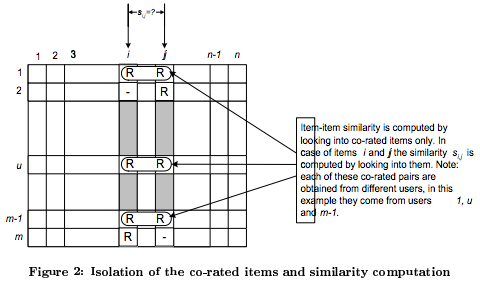*Imágenes del articulo de Sarwar et al. 2010, Item-Based Collaborative Filtering Recommendation Algorithms

1. Calcular Similaridad entre los Ítems
   • Cosine-Based Similarity
   • Correlation-Based Similarity
   • Adjusted Cosine Similarity
   • 1 - Jaccard distance (Das et al. 2007)
2. Cálculo de la Predicción
   • Suma ponderada (weighted Sum)
   • Regresión

• Cosine-Based Similarity \[sim(i,j) = cos(\vec{i},\vec{j}) = \frac{\vec{i}\cdot\vec{j}}{\|\vec{i}\|_2 \times \|\vec{j}\|_2}\]

• Correlation-Based Similarity \[sim(i,j) = \frac{\sum_{u \in U}{(R_{u,i}-\bar{R}_i)(R_{u,j}-\bar{R}_j)}}{\sqrt{\sum_{u \in U}{(R_{u,i}-\bar{R}_i)^2}}\sqrt{\sum_{u \in U}{(R_{u,j}-\bar{R}_j)^2}}}\]

• Adjusted Cosine Similarity \[sim(i,j) = \frac{\sum_{u \in U}{(R_{u,i}-\bar{R}_u)(R_{u,j}-\bar{R}_u)}}{\sqrt{\sum_{u \in U}{(R_{u,i}-\bar{R}_u)^2}}\sqrt{\sum_{u \in U}{(R_{u,j}-\bar{R}_u)^2}}}\]

• 1 - Jaccard distance (Das et al. 2007)

• Suma Ponderada (Weighted Sum)

\[\hat{P}_{u,i} = \frac{\sum_{all\ similar\ items,\ N}{(sim(i,N) \cdot R_{u,N})}}{\sum_{all\ similar\ items,\ N}{sim(i,N)}}\]

• Regresión \[\vec{R'}_{N} = \alpha \cdot \vec{R'}_{i} + \beta + \epsilon\]

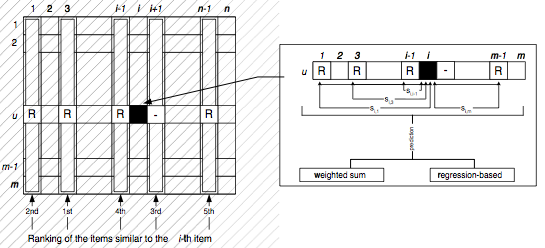
• Si bien este método podría considerarse memory-based, los autores de Sarwar et al. lo consideran model-based, donde el parámetro principal del modelo es K (número de ítems similares a considerar)

• Los autores usan MAE (Mean Absolute Error) para evaluar métodos.

• Resultados importantes para considerar en el análisis:

  • Efecto de la métrica de Similaridad
  • Sensitividad de la proporción Training/Test
  • Tamaño del vecindario (K)
  • Comparación con otros métodos

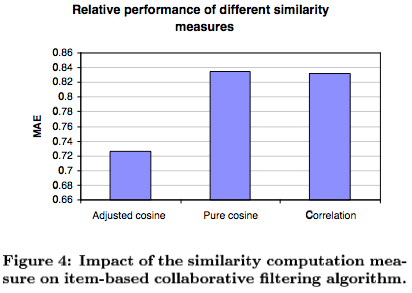
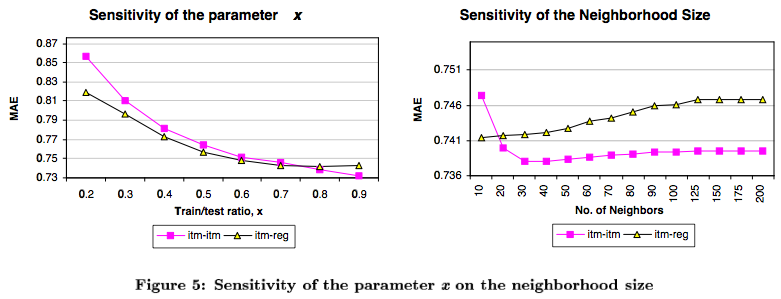
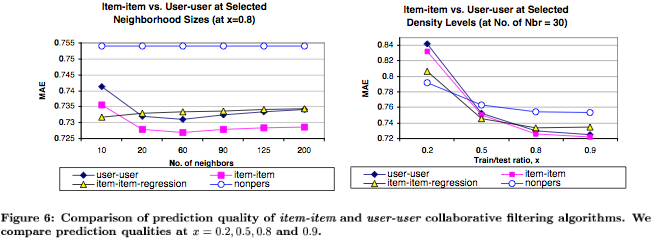
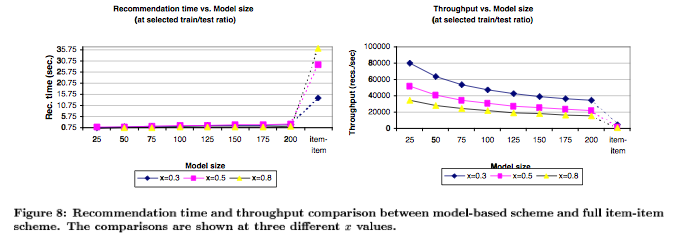
Leer Das et. al "Google News Personalization: Scalable Online Collaborative Filtering", que, para usando patrones de co-visita, incluye:

• Minhash: Probabilistic Clustering Method
• LSH (Locality Sensitive Hashing)
• MapReduce (para implementar MinHash)
• PLSI (Probabilistic Latent Semantic Indexing)

• Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2001, April). Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conference on World Wide Web (pp. 285-295). ACM.
• Lathia, N., Hailes, S., & Capra, L. (2008, March). The effect of correlation coefficients on communities of recommenders. In Proceedings of the 2008 ACM symposium on Applied computing (pp. 2000-2005). ACM.
• Breese, J. S., Heckerman, D., & Kadie, C. (1998, July). Empirical analysis of predictive algorithms for collaborative filtering. In Proceedings of the Fourteenth conference on Uncertainty in artificial intelligence (pp. 43-52). Morgan Kaufmann Publishers Inc.
• Das, A. S., Datar, M., Garg, A., & Rajaram, S. (2007, May). Google news personalization: scalable online collaborative filtering. In Proceedings of the 16th international conference on World Wide Web (pp. 271-280). ACM.